速さの問題の解き方！大切なのは「み・は・じの円」だけじゃない！？

小学校で習う算数で、難しくて大切な問題と言われて思い浮かぶのは、間違いなく速さの問題でしょう。

以前、塾に通っている中学１年生の生徒に質問をしたことがあります。

「小学校の算数で一番難しかったのは、何の単元だった？」

「割合かなぁ、速さかなぁ？」

「いや、絶対速さの問題やで！」

圧倒的に「割合」と「速さ」でした。それ以外の単元を答える生徒はほとんどいません。その他には、図形が苦手と答える生徒、小数の割り算と答える生徒がいた程度です。聞く前からだいたい答えの予想はついていたのですが、あえて聞いてみました。

「やっぱりそうか～」

「今ちょうど、小学5年生に割合、小学6年生に速さを教えているんやけど、どうすれば出来るようになる？」

「気合いかな！」「根性やろ！」

とまぁ、中学生に聞いてもこんな返事です。そのくらいみんな難しいと感じているのです。

 

小学5年生で習う割合、小学6年生で習う速さ、あまりいい思い出がない方も多いはずです。逆に「割合」と「速さ」を得意とするお子さんは、間違いなく算数に強いということが言えると思います。

そんなみんなが苦手としがちな単元ですが、絶対に避けて通るわけにはいきません。何としても乗り越えていく必要があります。

今回はその中の小学6年生で習う速さに焦点を当てて、基本的な問題から文章題の解き方やコツを紹介します。

 

速さの公式／「み・は・じ の円」

速さの問題を考える時には、「道のり」、「速さ」、「時間」の３つの要素が関係してきます。

そして小学校で習う速さの公式は、

「速さ」＝「道のり」÷「時間」

「道のり」＝「速さ」×「時間」

「時間」＝「道のり」÷「速さ」

 

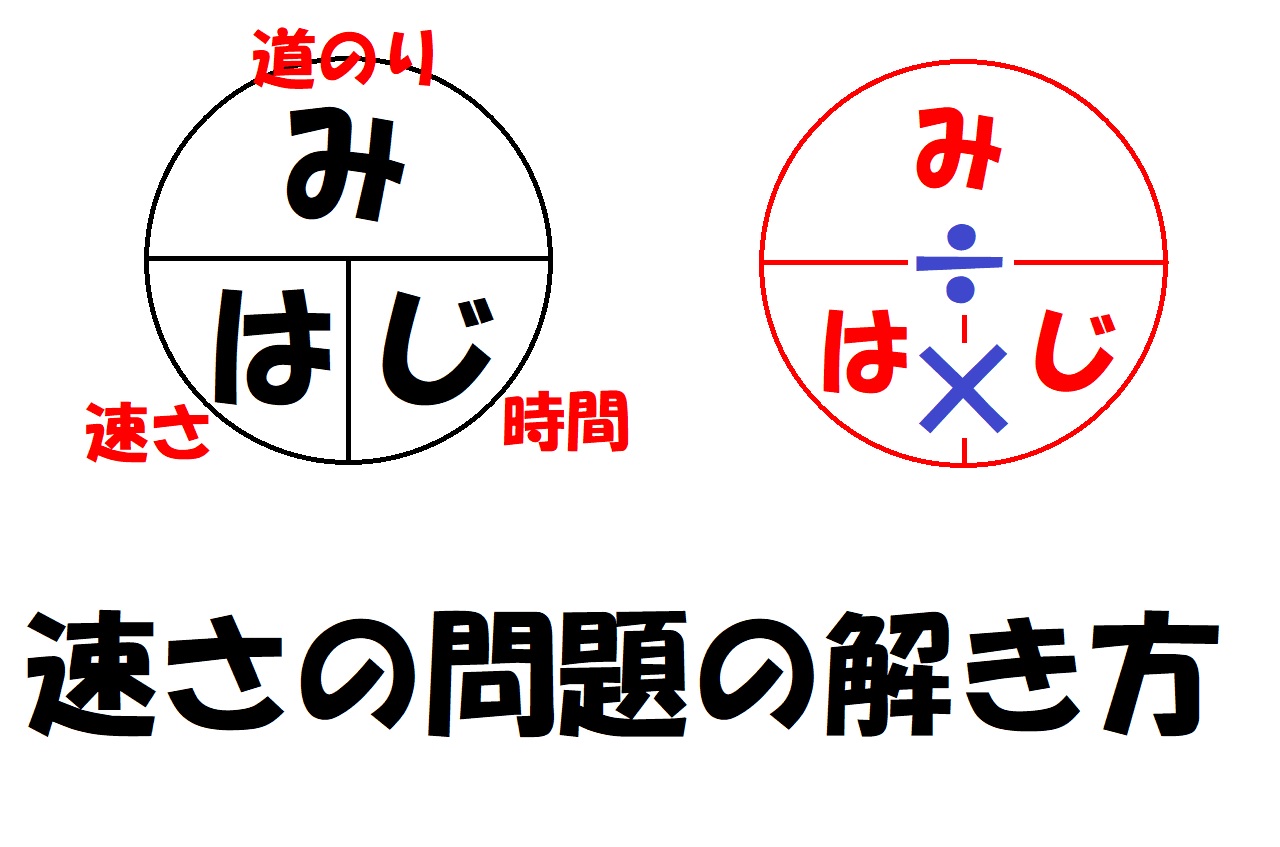
この3つになります。そして、これを覚える時に使うのが、有名な「み・は・じ の円」です。

この「み・は・じ の円」の使い方は必ずマスターしておきましょう。

速さの公式を間違うことなくことなく使いこなすには、この円で覚えるのが一番簡単なのです。どこの小学校でもこの方法と同じやり方で教えられていると思います。少なくとも私の勤めていた塾に通っていた生徒は、全員この方法で公式を覚えていました。

 

意外？「み・は・じ の円」の盲点

「み・は・じ の円」は速さの問題を解くときに、公式を思い出す方法として非常に役立つものです。それは間違いありません。

しかし、算数が得意な生徒になるほど、この「み・は・じの円」をかいていないことがわかります。

「えっ、どうして？」と思う人もいるかもしれませんが、私も「み・は・じの円」を書いた記憶はあまりありません。

 

算数の得意な生徒は、速さの問題を公式に当てはめることを考えずに解いています。無意識に公式を使っているともいえますが、少し違うのです。

簡単な問題で説明すると、

問　600mの道のりを15分で歩く速さは分速何mですか？

分速とは、1分間に進む道のりのこと。600mを15分で進むということは、1分当たりに進む道のりは、割り算を使えばいいから

600÷15＝40　答 40m

このような感じで解きます。

 

実際に算数の得意な生徒に、速さの問題を解くときに公式を意識しているかと聞いてみましが、ほとんどの生徒が「あまり意識していない！」と答えます。公式など考えることなく無意識の中で、×、÷ を判断しているのです。

「公式なんか考えなくても、問題を読んだらわかるし。」

「そんなの私には無理だ！」という声が聞こえてきそうですが、公式を使うなと言っているわけではありません。公式をしっかりと使いこなすことは大切なことです。

 

しかし、公式はあくまで公式であって、無意識のうちに使えるようになるのが一番なのです。慣れるまでは公式を使いながら解くのがいいかもしれませんが、いつまでも「み・は・じ の円」をかくのはやめた方がいいでしょう。少なくとも、書き出さずに頭の中で、思う描くようにしましょう。

 

単位をそろえる

速さの表し方の代表的な単位に、「時速」「分速」「秒速」があります。

また、時間を表す単位には、「時間」「分」「秒」があります。

そして、道のりを表す代表的な単位に、「km」「m」があります。

 

速さの問題では、この単位が違うことに惑わされて問題が解けない生徒が多いのです。単位をそろえることは、速さの問題を解くためには必要不可欠です。

 

典型的な間違いの例

このそれぞれの単位を、計算の中でそろえないと、とんでもない答えになってしまいます。

問　健太君は学校まで時速3kmの速さで歩いていくと30分かかります。学校までの道のりは何kmでしょうか。

「道のり」＝「速さ」×「時間」

だから、3×30＝90　答 90km

 

学校まで90kmもあるはずがない！

「どんだけ遠い学校に通っているねん！」「ありえないやろ！」と、突っこみが入ることは間違いない答えですね。

少し考えればおかしいことがわかると思うのですが、笑い話ではありません。算数の苦手な生徒は、こんな間違いを当たり前のようにするのです。

 

この場合は、単位を「時間」か「分」のどちらかにそろえる必要があります。

問　健太君は学校まで時速3kmの速さで歩いていくと30分かかります。学校までの道のりは何kmでしょうか。

速さは「時速」なのに、時間は「分」です。

時速3kmを分速50mに直すか、30分を0.5時間に直して計算します。

【分速で計算】50×30＝1500(m)　答 1.5kｍ

【時間で計算】3×0.5=1.5　答 1.5km

 

単位をそろえて計算することは、簡単なように見えて、きちんと意識するくせをつけないとなかなか難しいのです。そしてこの単位をそろえて計算することが、速さの問題をより難しくしている原因なのです。

 

単位の変換の方法

速さの問題を解くのに、単位を変換すること大切なのはよくわかったはずです。驚くような間違えた答えを出さないためにも、下の単位の変換の方法だけは、必ず覚えておきましょう！

 

・時間の単位の変換

 

・速さの単位の変換

 

・道のりの単位の変換

 

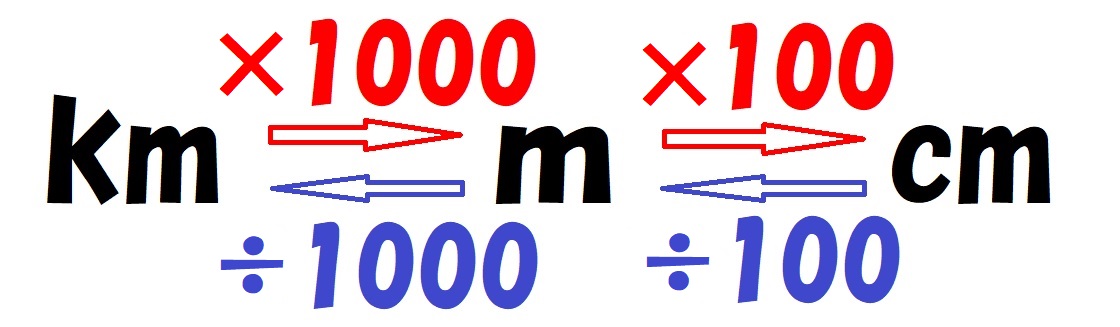
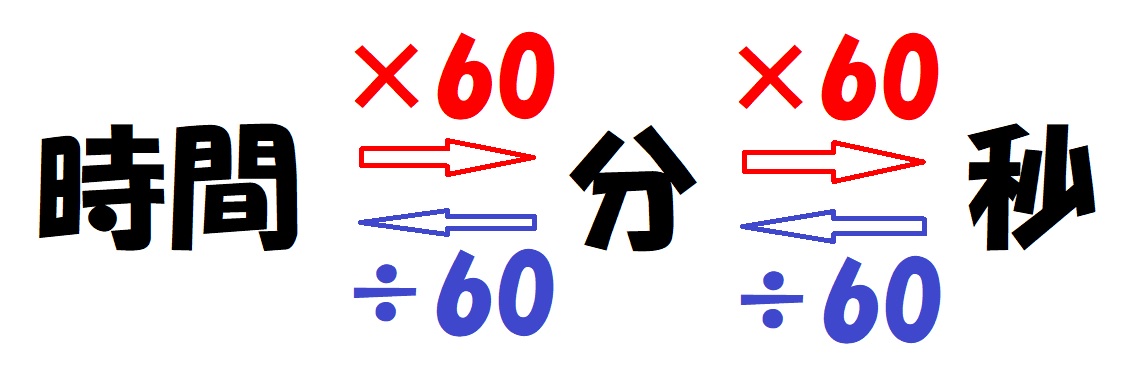
時間では、「時間」→「分」は ×60

速さでは、「時速」→「分速」は ÷60

時間と速さの単位の変換では、× と ÷ が逆になることに注意が必要です。

 

ここまでのことを完全に理解できれば、あとは練習あるのみです。この記事の初めに中学生が「気合い！」「根性！」と答えたのは、気合いと根性で練習することで出来るようになるという意味です。

速さの公式にしても、単位の変換にしても、毎回ノートに公式を書きださずにスムーズに解けるようにしましょう。

 

算数が得意な生徒は、算数の問題をどんどん解く。

そして算数がますます得意になる。そんな好循環が生まれます。

 

算数が苦手な生徒は、算数の問題をわからないからといって解かない。

そして算数がますます嫌いになる。そんな悪循環になります。

 

簡単な問題から繰り返し練習して、速さの問題を克服しましょう。たくさん問題を解けば、速さの問題にも慣れてくるのでスムーズに解けるようになります。

「練習、練習って、そればかり！」とよく言われますが、本当のことなのです。高校野球で甲子園に出ている選手でも、オリンピックに出ている選手でも、他人の何倍もの練習と努力を積み重ねているのは言うまでもないでしょう。

習いたての時はよく間違えていた九九が、今では当たり前に答えが出てくるのと同じことです。練習してやった分だけ必ず出来るようになるので、あきめずに頑張ろう。

 

文章題の解き方

速さの文章題は、他の単元の文章題と比べても難しい問題が多くあります。問題を作る側としては、基本的な問題から応用問題まで作成することが出来て、生徒の能力をよく知ることが出来る理想的な単元なのです。

その理由は、

・公式をしっかりと覚える必要がある

・単位の変換が必要になる

・線分図などをかかないとイメージしづらい

・数字が３つ４つと出てきて、どれを使うかわかりづらい

 

などの理由があげられます。逆に言えば、その原因を一つずつクリアしていけば、文章題も解けるようになります。

 

問題文を読み解く

速さの文章題の問題文を読み解くために必要なことは３つです。

１．単位をそろえる

２．数字などの重要な部分に線を引く

３．線分図をかく

 

この３つのことを徹底して行うようにしましょう。

特に線分図をかくことは、5年生で習った割合の問題や、中学校の方程式でも必要となります。問題を解くときには、いつも線分図をかくくせをつけておきましょう。

例題で説明すると

問　健太君の家から学校までは3kmあります。健太君は時速3kmで家を出発し、30分歩きました。学校まであと何mありますか。

 

この問題はまず、下のように線を引きます。

問　健太君の家から学校までは3kmあります。健太君は時速3kmで家を出発し、30分歩きました。学校まであと何mありますか。

注意すべきポイントは、3km、時速3km、30分、あと何ｍの部分です。

時速と分、kmとm、しっかりと区別をつけておきましょう。

 

そして線分図はこのようになります。

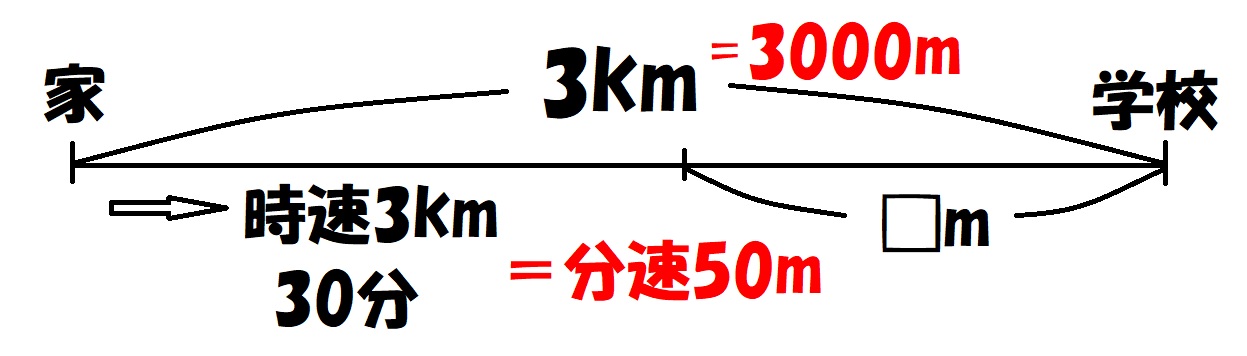
こんな風に線分図がかけていれば、問題文がよく整理されてわかりやすいと思います。

ここまで出来れば、問題は半分以上解けたも同然です。

50×30＝1500 ←進んだ道のり

3000－1500＝1500　答 1500ｍ

 

問題を解くために必要なこと、線を引く！線分図をかく！をしっかり守って練習しましょう。そして、問題に慣れてくれば、簡単な問題は線分図をかかなくても解けるようになるでしょう。

 

ただし、問題文の重要な部分に線を引くことは続けた方がいいと思います。それは、線を引く作業をするだけで、問題文をきちんと読み込むことが出来て、うっかりミスをなくすことが出来るからです。算数の得意な生徒ほど、問題を自分勝手に読み間違えてしまうことが多いものです。

 

まとめ

今回は算数の速さの問題の解き方を説明しました。

・速さの公式

・単位をそろえる

・問題文に線を引く

・線分図をかく

 

などなど気を付けることはたくさんあります。速さは本当に難しい単元になりますが、練習を繰り返すことで必ず解けるようになります。

どんな単元の問題もそうですが、基本的な問題から応用問題へ。繰り返し練習することが、その単元を得意にする一番の方法なのです。

 

苦手だから勉強しないでは、ずっと苦手なままです。

苦手だからこそ、早めに克服しましょう。

 

小学校の算数の最大の難所が速さの単元です。そしてこの速さの問題は、中学校になってからも文字式、方程式などの単元で必要になってきます。

努力すれば必ず成果は出てきます。速さを克服して、算数を得意科目にしよう。