塾の中学1年生の生徒に質問をしました。小学生の算数の中で難しいと思うのは、何の単元?
答えは聞く前からわかっているのですが、あえて聞いてみます。ほぼ全員が口をそろえて言うのが、
「割合の問題」「速さの問題」
圧倒的にこの2つでした。それ以外の単元を答える生徒はほとんどいません。その他には、図形が苦手と答える生徒、小数の割り算と答える生徒がいた程度です。
「やっぱりそうか~」
「今ちょうど、小学5年生に割合、小学6年生に速さを教えているんやけど、どうすれば出来るようになる?」
「気合やで!」「いや、根性かな?」
とまぁ、中学生に聞いてもこんな返事です。
小学5年生で習う割合、小学6年生で習う速さ、あまりいい思い出がない方も多いはずです。逆に割合と速さを得意とするお子さんは、間違いなく算数に強いということが言えると思います。
そうなんです。算数の苦手なお子さんは、必ずと言っていいほど割合と速さでつまづいています。
そんなみんなが苦手としがちな単元ですが、絶対に避けて通るわけにはいきません。何としても乗り越えていく必要があります。
今回はその中の小学5年生で習う割合に焦点を当てて、基本的な問題から文章題の解き方やコツを紹介します。
基本的な割合の問題

割合の問題を考える時には、「くらべられる量」、「もとにする量」、「割合」の3つが関係してきます。
もうこの言葉の時点で「意味不明!」と投げ出したくなりますね。でも我慢してついてきてください。
小学校で習う公式は3つあります。
「割合」=「くらべられる量」÷「もとにする量」
「くらべられる量」=「もとにする量」×「割合」
「もとにする量」=「くらべられる量」÷「割合」
教科書には、公式としてこれを覚えるように書いてあるのです。はい、ますます割合が嫌いになりそうですね。なんでこんなにややこしいのでしょう。
くらべられる量?もとにする量?
しかし、はっきり言って「くらべられる量」や「もとにする量」と言われても、いまいちよくわかりません。本当に意味不明です。
特に割合を苦手とする生徒の場合、「くらべられる量」と「もとにする量」の区別がついていないことがほとんどです。しかしこれを乗り越えなければ、割合の問題を解くことは出来ない。あきらめずに頑張りましょう。
簡単な例題で説明します。
問 40本の鉛筆は、100本の鉛筆の何%ですか?
この問題で40本が「くらべられる量」、100本が「もとにする量」、何%が割合になります。
うーん、よくわからない。こりゃ、ダメだ。
そんな声が聞こえてきそうです。
問題文をもっとかみ砕いて説明するとこうなります。
問 40本の鉛筆というのは、100本の鉛筆をもとにすると何%の割合ですか?
これでどうでしょうか。少しはわかりやすくなったかな?
この「くらべられる量」や「もとにする量」、「割合」が何を指すかわからないと問題を解くことが難しいのです。
何度も何度も問題を読んで、どれが「くらべられる量」で「もとにする量」かをしっかりと考えましょう。文章の下に線を引いて「く」、「も」、「わ」と書き込んでいってもいいと思います。
そして公式に当てはめるわけですが、公式を覚えるのもまた難しい。
そこで登場するのが「く・も・わの 円」です。
く・も・わ の円
「く・も・わの円」とは、公式をわかりやすく円で表したものです。
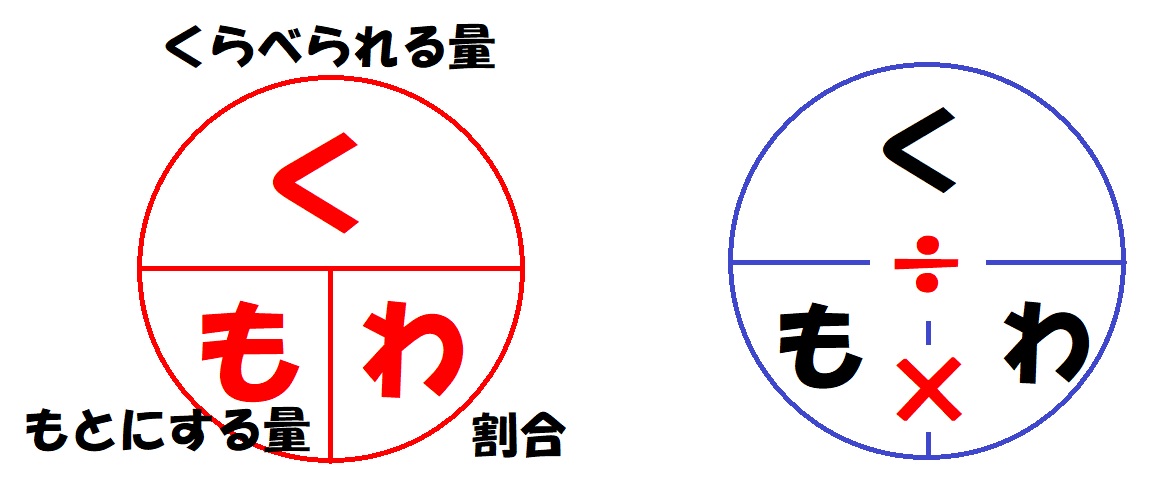
6年生の速さの問題にも同じような「み・は・じの円」が出てくるのですが、それも同じ考え方で使うことが出来ます。
この円を覚えておけば、割合の公式で迷うことがなくなります。
このような円の使い方は6年生の速さも同じということは、割合と速さは同じような考え方で解くことが出来るのです。
つまり、5年生の割合を攻略できれば、6年生の速さも攻略できる!ということになります。
の → ×、は → =、の考え方を覚える
次の方法は、問題文の中の、「の → ×」、「は → =」、へと置き換えて計算する方法です。これは基本問題には絶大な効果を発揮します。
これさえ知っていれば、基本問題は楽勝です!
問 40本の鉛筆は、100本の鉛筆の何%ですか?
→ 40 = 100 × □
□=0.4 つまり 40% となります。
もう一問やってみましょう。
問 60円の60%は、何円ですか?
→ 60×0.6=□
□=36 つまり 36円 となります。
簡単な問題であれば、この、「の → ×」、「は → =」、へと置き換えて計算する方法でほとんどの問題が解くことが出来ます。
しかし、□を求めるためには逆算が必要になってきますので、そこは注意して下さい。
それでも解けない割合の問題
「く・も・わ の円」や「の → ×」、「は → =」の置き換えの方法をしっかりとマスターできたでしょうか?ここまでは、まだ基本中の基本です。これだけが理解できていても、まだ割合は解けません。
割合の攻略に必要なこと
それは文章の読解力です。
「はい、それはわかってます。」
その文章の読解力をつけるにはどうすればいいか?
「何か必殺技を教えてください!」
残念ながらありません。簡単な問題から始めて、問題演習を繰り返すのが一番の近道です。
割合の問題を解くときに、慣れてくると「これが、くらべられる量で・・・」というようなことは意識しません。ほとんど無意識のうちに公式に当てはめて計算しています。
そのために必要なこと。
練習です。
割合を苦手とするほとんどの人が、苦手だから練習しない、練習しないから出来るようにならないの悪循環になっています。
まずは一番簡単な、3パターンの問題から見てみましょう。
1.400円の60%は何円ですか。
くらべられる量を求める
2.240円は400円の何%ですか。
割合を求める
3.何円の60%が240円になりますか。
もとにする量を求める
このパターンの問題で、割合の公式がスラスラと使えるように練習します。
さっとできるまで、何十問、何百問と練習して下さい。この基本問題がしっかりと出来るようになると、簡単な文章問題も解けるようになります。
文章題の読解
文章題を解くためには、次の2つの方法で取り組みます。文章題が出来ないお子さんは、この方法がまず出来ていません。
1.文章をよく読んで、数字の前後の大切な部分に線を引く
2.線分図、面積図で表す
問 健太君は600円持って買い物に出かけました。そして持っているお金の40%を使って本を買いました。本の値段はいくらでしょうか。
この問題であれば、
問 健太君は600円持って買い物に出かけました。そして持っているお金の40%を使って本を買いました。本の値段はいくらでしょうか。
このように線が引けるようになりましょう。線を引く!
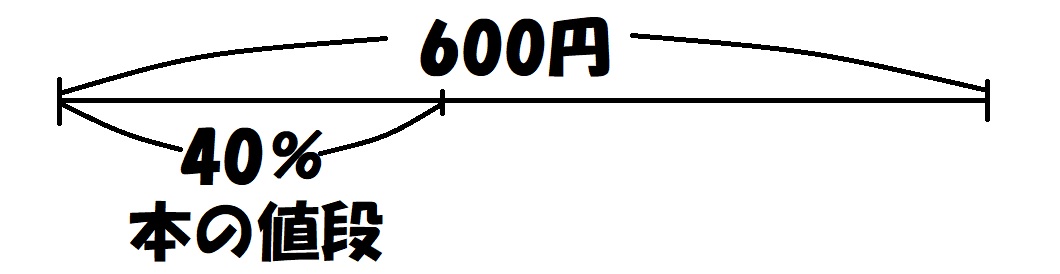
そしてこのような線分図がかけるといいですね。線分図をかく!
この作業を問題を解くときに絶対にさせて下さい。初めのうちは、どんな簡単な問題でも絶対にさせて下さい。
数字などの大切な部分に線を引く、線分図をしっかりかく、この2点は難しい問題を解くときにも必ず役に立ちます。
そして、他の単元の文章題を解くときにも役に立ちます。
とにかく、線を引く、線分図をかく、これを徹底します。割合を苦手としているお子さんの場合には、親御さんがサポートしてあげて下さい。
線の引き方、線分図の書き方、間違っていれば、その時に理由を添えて訂正してあげて下さい。同じ問題でもいいです。何度も何度も練習しましょう。
割合はそんなに簡単ではない
割合の単元は、本当に小学生の算数の中でも最大の山場といっても過言ではありません。ですから、そんなに簡単には理解できないでしょう。
でも、あきらめてはいけません。コツコツと練習を重ねると、必ず解けるようになってきます。文章が読めてくるようになるのです。
割合は難しい。だからこそ、割合をスムーズに理解できるようになれば、かなり算数の力が付いたと思っていいでしょう。しっかりと基本問題から練習しましょう。
まとめ
今回は割合の解き方のコツを紹介しました。
「く・も・わ の円」や「の → ×、は → =」の置き換えの方法は、最低限必ず理解しておきましょう。
そして、他の単元にも共通して言えることですが、割合が難しくても、練習することによって必ず理解できるようになります。
文章題は特に苦手とする生徒が多いので、逆にそれを克服すれば大きな強みとなります。
基本的な考え方である、
・問題文の大事な部分に線を引く
・線分図などを使って表す
この2点だけは、どんな問題でも絶対に練習するようにしましょう。
割合を克服できれば、6年生で習う速さも同じように理解できることでしょう。
あきらめずに練習すること。
基本問題から文章問題へと、徐々にステップアップすること。
何としてでも割合をマスターして、算数を得意科目にしよう!

